materibelajar.com - Transformasi geometri merupakan salah satu materi matematika yang membahas mengenai dengan perpidahan bidang geometri dari posisi semula ke posisi bayangan dengan melakukan proses translasi, rotasi, dilatasi dan refleksi.
Pada laman ini kita akan belajar lebih jauh memahami bagaimana menghitung transformasi geometri rekfleksi atau pencerminan dari bidang geometri dengan menggunakan contoh soal yang disertai pembahasan berikut.
1. Diketahui sebuah titik a(-2, 8) dilakukan pencerminan terhadap sumbu y dan menghasilkan bayangan titik a'. Hitunglah letak posisi bayangan titik a' dengan menggunakan rumus!
penyelesaian
a(-2, 8) terhadap sumbu y
a(x, y) → sumbu y → a'(-x, y)
a(-2, 8) → a'(-(-2), 8)
a(-2, 8) → a'(2, 8)
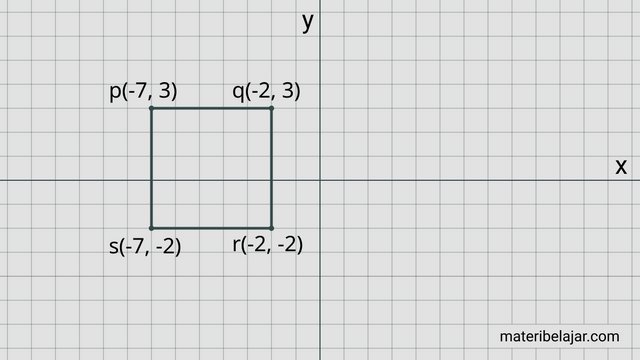
2. Jika sebuah bidang berbentuk persegi dengan koordinat berturut-turut p(-7, 3), q(-2, 3), r(-2, 2) dan s(-7, -2) seperti berikut.
Hitung koordinat bayangan persegi tersebut apabila direfleksikan terhadap sumbu y!
penyelesaian
gunakan rumus untuk mencari bayangan pada sumbu y
a(x, y) → sumbu y → a'(-x, y)
hitung masing-masing bayangan pada titik p, q, r dan s.
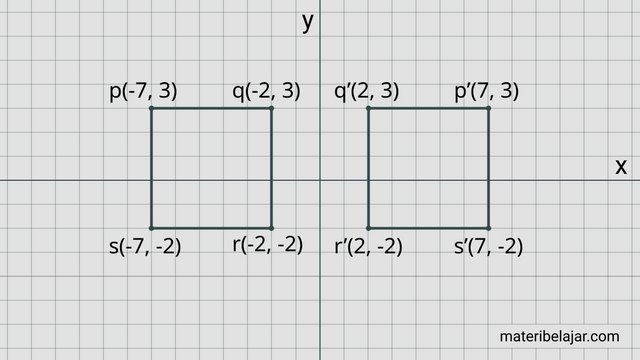
p(-7, 3) → p'(-(-7), 3)
p(-7, 3) → p'(7, 3)
q(-2, 3) → q'(-(-2), 3)
q(-2, 3) → q'(2, 3)
r(-2, -2) → r'(-(-2), -2)
r(-2, -2) → r'(2, -2)
s(-7, -2) → s'(-(-7), -2)
s(-7, -2) → s'(7, -2)
Setelah kita hitung, diperoleh bayangan persegi ke dalam bidang koordinat seperti berikut.
3. Carilah letak bayangan titik j(2, 2) apabila dilakukan pencerminan terhadap garis x = -2!
penyelesaian
j(2, 2) terhadap garis x = -2
dengan menggunakan rumus refleksi terhadap garis x = a kita dapat menghitungnya sebagai:
a(x, y) → garis x = i → a'(2i - x, y)
j(2, 2) → j'(2(-2) - 2, 2)
j(2, 2) → j'(-6, 2)
Jadi letak bayangan titik j terletak pada j'(-6, 2).
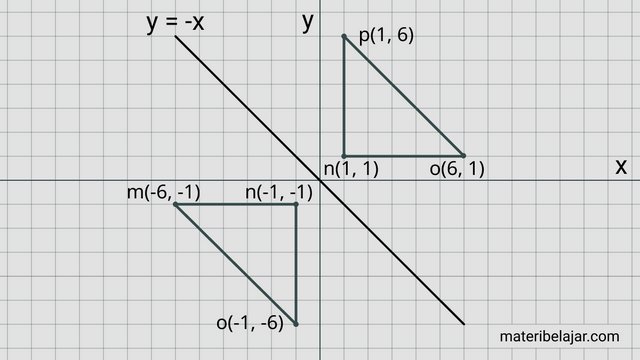
4. Sebuah bangun datar segitiga siku-siku yang dibentuk dari gabungan titik koordinat berturut-turut m(-6,-1), n(-1, -1) dan o(-1,-6).
Berapakah letak koordinat bayangan segitiga tersebut apabila direfleksikan terhadap sumbu y = -x?
penyelesaian
sama seperti soal sebelumnya, kita terlebih dahulu hitung bayangan dari tiap titik namun terhadap sumbu y = -x.
a(x, y) → sumbu y = -x → a'(-y, -x)
m(-6, -1) → m'(-(-1), -(-6))
m(-6, -1) → m'(1, 6)
n(-1, -1) → n'(-(-1), -(1))
n(-1, -1) → n'(1, 1)
o(-1, -6) → o'(-(-6), -(-1))
o(-1, -6) → o'(1, 6)
Jadi diperoleh bayangan setelah direfkleksikan berturut-turut m(1, 6), n(1, 1) dan o(1, 6).
5. Sebuah persamaan garis lurus 3x + 2y = 6 dilakukan pencerminan terhadap sumbu x, hitunglah persamaan garis lurus tersebut setelah dilakukan pencerminan!
penyelesaian
a(x, y) → sumbu x → a'(x, -y)
sehingga diperoleh:
x = x'
y = -y'
subtitusikan ke dalam persamaan.
3(x') + 2(-y') = 6
3x' - 2y' = 6
Jadi diperoleh persamaan garis setelah dilakukan refleksi terhadap sumbu x menjadi 3x - 2y = 6.
6. Sebuah persamaan lingkaran yang berpusat pada (2, 8) dan memiliki jari-jari sebesar 3 satuan dicerminkan terhadap sumbu x = y. Hitunglah persamaan lingkaran tersebut setelah dilakukan pencerminan!
penyelesaian
Terlebih dahulu kita hitung bayangan dari titik pusat lingkaran tersebut.
a(x, y) → sumbu x = y → a'(y, x)
a(2, 8) → a'(8, 2)
Kemudian hitung bayangan persamaan lingkaran dengan mensubtitusikan a'(8, 2) dan r = 3 ke dalam rumus persamaan lingkaran.
(x - a)2 + (y - b)2 = r2
(x - 8)2 + (y - 2)2 = 32
(x - 8)2 + (y - 2)2 = 9
Jadi diperoleh bayangan persamaan lingkaran (x - 8)2 + (y - 2)2 = 9.